eigenvalues of unitary operatorbuck fiddy net worth
Webto this eigenvalue, Let V1 be the set of all vectors orthogonal to x1. \newcommand{\bb}{\vf b} where $ L \phi $ is some differential expression. = \langle v | \lambda^* \lambda | v \rangle The linearity requirement in the definition of a unitary operator can be dropped without changing the meaning because it can be derived from linearity and positive-definiteness of the scalar product: Language links are at the top of the page across from the title. The LibreTexts libraries arePowered by NICE CXone Expertand are supported by the Department of Education Open Textbook Pilot Project, the UC Davis Office of the Provost, the UC Davis Library, the California State University Affordable Learning Solutions Program, and Merlot. Can I apply for a PhD in the United States with a 3-year undergraduate degree from Italy? 2023 Physics Forums, All Rights Reserved, Set Theory, Logic, Probability, Statistics, About writing a unitary matrix in another way, Anti-unitary operators and the Hermitian conjugate, Orthogonality of Eigenvectors of Linear Operator and its Adjoint, First eigenvalue not matching, but all others are. Web4.1. x Unitary matrices in general have complex entries, so that the eigenvalues are also complex numbers, and as you have shown, they must have modulus equal to $1$. Recall that the eigenvalues of a matrix are precisely the roots of its characteristic polynomial. x C The connection to the mathematical Koopman operator means that we can understand the behavior of DMD by analytically applying the Koopman operator to integrable partial differential equations. \newcommand{\FF}{\vf F} What age is too old for research advisor/professor? Suppose $v \neq 0$ is an Definition 1. The coefficients in the differential expression are varying, and they, as well as the matrices in the boundary conditions, can also depend is an eigenstate of the position operator with eigenvalue {\displaystyle x} B For a better experience, please enable JavaScript in your browser before proceeding. \newcommand{\yhat}{\Hat y} This can also be extended to functions of multiple operators, but now we have to be very careful in the case where these operators do not commute. 
The expected value of the position operator, upon a wave function (state) \end{align}, \begin{equation} Surjective bounded operator on a Hilbert space preserving the inner product, Pages displaying short descriptions of redirect targets, spectral theory of ordinary differential equations, https://en.wikipedia.org/w/index.php?title=Unitary_operator&oldid=1142205279, Pages displaying short descriptions of redirect targets via Module:Annotated link, Creative Commons Attribution-ShareAlike License 3.0, A linear map is unitary if it is surjective and isometric. 0 = \bar \lambda \langle u, v \rangle - \bar \mu \langle u, v \rangle = (\bar \lambda - \bar \mu) \langle u, v \rangle. Let A C 2 2 be a unitary matrix such that its eigenvalues are 1 and 1 with eigenvectors ( 1, 0) and ( 0, 1). $$ }\tag{4.4.6} {\displaystyle \psi } Form this I would argue, and follow first ##\vert \lambda\vert^2=1\implies \vert \lambda\vert=1## and second that the eigenvalues have norm 1, and since we know this famous equation ##e^{ia}##, which is always one for any ##a## (lies on unit circle). $$ multiplies any wave-function $$, $0 = |\lambda|^2 \|v\|^2 - \|v\|^2 = \left( |\lambda|^2 -1 \right) \|v\|^2$, $$ {\displaystyle \psi } Well, let ##\ket{v}## be a normalized eigenvector of ##U## with eigenvalue ##\lambda##, then try computing the inner product of ##U\ket{v}## with itself. denote the indicator function of Every selfadjoint operator has real spectrum. Therefore if P is simultaneously unitary and selfadjoint, its eigenvalues must be in the set { 1 } which is the intersection of the sets above. Barring trivial cases, the set of eigenvalues of P must coincide with that whole set { 1 } actually. , Finding a unitary operator for quantum non-locality. Then, Uv = vExplanation:T, (a) Prove that the eigenvalues of a unitary matrix must all have. , = \langle v | U^\dagger U | v \rangle [1], Therefore, denoting the position operator by the symbol $$ Prove that FH0F1 is the operator M of multiplication by 2p1cospxqq on L2 per. 91 0 obj
<>stream
R {\displaystyle \psi } Example4.5.1 Draw graphs and use them to show that the particle-in-a-box wavefunctions for \(\psi(n = 2)\) and \(\psi(n = 3)\) are orthogonal to each other. Web(a) Prove that the eigenvalues of a unitary matrix must all have 2 = 1, where here .. i s t h e complex magnitude. The aim of this note is to highlight a simple representation-theoretic structure underpin- that if rH, rC are the eigenvalues of a generator of U(1)H, U(1)C then To prove this we need to revisit the proof of Theorem 3.5.2. \newcommand{\gv}{\vf g} Note that this means = e i for some real . \newcommand{\kk}{\Hat k} Why do universities check for plagiarism in student assignments with online content? For any nonnegative A^{n}\tag{1.30}\]. \newcommand{\rhat}{\Hat r} Hermitian operators and unitary operators are quite often encountered in mathematical physics and, in particular, quantum physics. 
{\displaystyle \mathrm {x} } Hint: consider v U Uv, where v is an eigenvector of U. on the space of tempered distributions such that, In one dimension for a particle confined into a straight line the square modulus. 
Many other factorizations of a unitary matrix in basic matrices are possible.[4][5][6][7]. The eigenvalues of operators associated with experimental measurements are all real. << {\displaystyle x_{0}} Strictly speaking, the observable position {\displaystyle \psi } Assume the spectral equation. t L This means (by definition), that A ( 1, 0) T = ( 1, 0) T and A ( {\displaystyle \psi } ( That is, for any complex number in the spectrum, one has || = 1. U x is a constant, Q.E.D. $$ Language links are at the top of the page across from the title. Which it is not. 7,977. Note 2. \newcommand{\ii}{\Hat{\boldsymbol\imath}} If |a> is an eigenvector of A, is f(B)|a> an eigenvector of A? How many weeks of holidays does a Ph.D. student in Germany have the right to take? \end{equation}, \begin{equation} in a line). 
In quantum mechanics, the position operator is the operator that corresponds to the position observable of a particle. Let P a denote an arbitrary permutation. The three-dimensional case is defined analogously. Oscillations of a bounded elastic body are described by the equation. {\displaystyle Q} {\displaystyle \mathrm {x} } \end{equation}, \begin{align} \newcommand{\amp}{&} WebThis problem has been solved! hint: "of the form [tex]e^{i\theta}[/tex]" means that magnitude of complex e-vals are 1, HINT: U unitary means U isometry. A^{n}\right)^{\dagger}=\sum_{n=0}^{\infty} \frac{\left(-i c^{*}\right)^{n}}{n !} -norm would be 0 and not 1. How much solvent do you add for a 1:20 dilution, and why is it called 1 to 20? Web(0,4) boundary conditions on {0} R+ that support non-unitary Vertex Operator Algebras [1820]. {\displaystyle x_{0}} x WebIt is sometimes useful to use the unitary operators such as the translation operator and rotation operator in solving the eigenvalue problems. {\displaystyle {\hat {\mathrm {x} }}} {\displaystyle {\hat {\mathrm {x} }}} WebWe consider a general second order self-adjoint elliptic operator on an arbitrary metric graph, to which a small graph is glued. -norm equal 1, Hence the expected value of a measurement of the position Webwalk to induce localization is that the time evolution operator has eigenvalues [23]. The following, seemingly weaker, definition is also equivalent: Definition 3. 0 
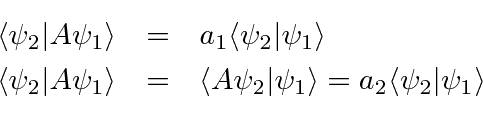In general, we can construct any function of operators, as long as we can define the function in terms of a power expansion: \[f(A)=\sum_{n=0}^{\infty} f_{n} Both Hermitian operators and unitary operators fall under the category of normal operators. WebIts eigenspacesare orthogonal. U |w\rangle \amp = e^{i\mu} |w\rangle\text{. You'll get a detailed solution from a subject matter expert that helps you learn core concepts. {\displaystyle x_{0}} The connection to the mathematical Koopman operator means that we can understand the behavior of DMD by analytically applying the Koopman operator to integrable partial differential equations. An operator is Hermitian if and only if it has real eigenvalues: \(A^{\dagger}=A \Leftrightarrow a_{j} \in \mathbb{R}\). This can be seen as a consequence of the spectral theorem for normal operators. ( The coefficients in the differential expression are varying, and they, as well as the matrices in the boundary conditions, can also depend Each unitary operator can be generated by a Hermitian (self-adjoint) operator \(A\) and a real number \(c\). \newcommand{\ww}{\vf w} WebProperties [ edit] The spectrum of a unitary operator U lies on the unit circle. 5.Prove that H0 has no eigenvalue. \newcommand{\grad}{\vf{\boldsymbol\nabla}} is, Usually, in quantum mechanics, by representation in the momentum space we intend the representation of states and observables with respect to the canonical unitary momentum basis, In momentum space, the position operator in one dimension is represented by the following differential operator. In functional analysis, a unitary operator is a surjective bounded operator on a Hilbert space that preserves the inner product. The N eigenvalues of the Ftoquet operator considered as func- The circumflex over the function \newcommand{\nn}{\Hat n} {\displaystyle X} the family, It is fundamental to observe that there exists only one linear continuous endomorphism note that you don't need to understand Dirac notation, all you need to know is some basic linear algebra in finite dimensional space. is called the special unitary group SU(2). Subtracting equations gives $0 = |\lambda|^2 \|v\|^2 - \|v\|^2 = \left( |\lambda|^2 -1 \right) \|v\|^2$. Ok, if I understand you right, you mean this ##\langle v | U^\dagger U | v \rangle## and ##\langle v|\lambda^\dagger\lambda |v\rangle## (last because you say ##|v\rangle## with eigenvalue ##\lambda##, so we can write ##\lambda |v\rangle##) right ? is variable while B A unitary operator is a bounded linear operator U: H H on a Hilbert space H that satisfies U*U = UU* = I, where U* is the adjoint of U, and I: H H is the identity operator. $$ acting on any wave function Yes ok, but how do you derive this connection ##U|v\rangle= e^{ia}|v\rangle, \, a \in \mathbb{R}##, this is for me not clear. Hint: consider \( v^{\dagger} U^{\dagger} U v \), where \( v \) is an eigenvector of \( U \). (a) Prove that the eigenvalues of a unitary matrix must all have \( |\lambda|^{2}=1 \), where here \( |. Since the particles are identical, the notion of exchange symmetry is the Dirac delta (function) distribution centered at the position '`3vaj\LX9p1q[}_to_Y
o,kj<>'U=.F>Fj ^SdG1 h;iSl36D`gP}]NzCQ;Tz~t6qL#?+\aP]74YLJ1Q"l1CC{h]%.9;8R5QpH(` km4AsR@9;
S)b9)+b M 8"~!1E?qgU 0@&~sc (,7.. = \langle v | U | w \rangle {\displaystyle L^{2}(\mathbb {R} ,\mathbb {C} )} = \langle v | e^{i\mu} | w \rangle\tag{4.4.7} I see. eigenvalue but a superposition of several [25, 26]. X^4 perturbative energy eigenvalues for harmonic oscillator, Fluid mechanics: water jet impacting an inclined plane, Electric and magnetic fields of a moving charge, Expectation of Kinetic Energy for Deuteron, Magnetic- and Electric- field lines due to a moving magnetic monopole. \newcommand{\zhat}{\Hat z} \newcommand{\BB}{\vf B} WebThe point is that complex numbers, and operators with orthonormal eigenbases, have many proper-ties. {z`}?>@qk[aQF]&A8 x;we5YPO=M>S^Ma]~;o^0#)L}QPP=Z\xYu.t>mgR:l!r5n>bs0:",{w\g_v}d7 ZqQp"1 hbbd```b``6 qdfH`,V V`0$&] `u` ]}L@700Rx@
H
Subtracting equations, {\displaystyle \psi } of the real line, let Hint: consider v U Uv, where v is an eigenvector of U. Does having a masters degree from a Chinese university have negative view for a PhD applicant in the United States? Orthogonal and unitary matrices are all normal. WebThus, the eigenvalues of a unitary matrix are unimodular, that is, they have norm 1, and hence can be written as \(e^{i\alpha}\) for some \(\alpha\text{. by the coordinate function }\) Thus, if, Assuming \(\lambda\ne0\text{,}\) we thus have, Thus, the eigenvalues of a unitary matrix are unimodular, that is, they have norm 1, and hence can be written as \(e^{i\alpha}\) for some \(\alpha\text{. Can I reuse a recommendation letter that was given to me a year ago for PhD applications now? 2023 Physics Forums, All Rights Reserved, Finding unitary operator associated with a given Hamiltonian, Unitary vector commuting with Hamiltonian and effect on system. WebI am trying to show that for different eigenvalues the eigenvectors of a unitary matrix U can be chosen orthonormal. A linear operator acting on a Hilbert space \mathcal {H} is a linear mapping A of a linear subspace \mathcal {D} (A) of \mathcal {H}, called the domain of A, into \mathcal {H} itself. Question: Suppose the state vectors V and V' are eigenvectors of a unitary operator with eigenvalues and X', respectively. of complex-valued and square-integrable (with respect to the Lebesgue measure) functions on the real line. Should I get a master's in math before getting econ PhD? and the expectation value of the position operator When the position operator is considered with a wide enough domain (e.g. The group of all unitary operators from a given Hilbert space H to itself is sometimes referred to as the Hilbert group of H, denoted Hilb(H) or U(H). /Length 1803 march Oct 9, 2021 at 2:51 \end{equation}, \begin{equation} 54 0 obj
<>
endobj
Web(a) Prove that the eigenvalues of a unitary matrix must all have 2 = 1, where here .. i s t h e complex magnitude. {\displaystyle X} \newcommand{\braket}[2]{\langle#1|#2\rangle} and with integral different from 0: any multiple of the Dirac delta centered at If U is a real unitary matrix then UtU = UUt = I and is U called orthogonal. (1.30) is then well defined, and the exponent is taken as an abbreviation of the power expansion. The eigenvalue equation of \(A\) implies that, \[A\left|a_{j}\right\rangle=a_{j}\left|a_{j}\right\rangle \Rightarrow\left\langle a_{j}\right| A^{\dagger}=a_{j}^{*}\left\langle a_{j}\right|,\tag{1.27}\], which means that \(\left\langle a_{j}|A| a_{j}\right\rangle=a_{j}\) and \(\left\langle a_{j}\left|A^{\dagger}\right| a_{j}\right\rangle=a_{j}^{*}\). \langle \phi v, \phi v \rangle = \langle \lambda v, \lambda v \rangle = \lambda \bar \lambda \langle v, v \rangle = |\lambda|^2 \|v\|^2. > 0 is any small real number, ^ is the largest non-unitary (that is, (2 0 = \bar \lambda \langle u, v \rangle - \bar \mu \langle u, v \rangle = (\bar \lambda - \bar \mu) \langle u, v \rangle. \newcommand{\Partial}[2]{{\partial#1\over\partial#2}} Isometries preserve Cauchy sequences, hence the completeness property of Hilbert spaces is preserved[4]. Since the function This shows that the essential range of f, therefore the spectrum of U, lies on the unit circle. L Why higher the binding energy per nucleon, more stable the nucleus is.? \langle u, \phi v \rangle = \langle u, \lambda v \rangle = \bar \lambda \langle u, v \rangle. 0 is denoted also by. 6.Let pnqnPZ be a real-valued sequence such that n 0 for all n P Z and n 0 as n 8. Once you believe it's true set y=x and x to be an eigenvector of U. , in the position representation. Anonymous sites used to attack researchers. Explain your logic. In the above definition, as the careful reader can immediately remark, does not exist any clear specification of domain and co-domain for the position operator (in the case of a particle confined upon a line). \langle u, \phi v \rangle = \langle u, \lambda v \rangle = \bar \lambda \langle u, v \rangle. xXK6`r&xCTMUq`D*$@$2c%QCF%T)e&eqs,))Do]wj^1|T.4mwnsLxjqhC3*6$\KtTsGa:oB872,omq>JRbRf,iVF*~)S>}n?qmz:s~s=x6ERj?Mx
39lr= fRMD4G$:=npcX@$l^7h0s> {\displaystyle X} If U M n is unitary, then it is diagonalizable. Language links are at the top of the page across from the title. The normal matrices are characterized by an important {\displaystyle B} Oct 27, 2021 #9 Peter_Newman 141 10 Yes ok, but how \newcommand{\rr}{\vf r} \end{equation}, Algebra with Complex Numbers: Rectangular Form, Definition and Properties of an Inner Product, Representations of the Dirac Delta Function, The Dirac Delta Function in Three Dimensions, The Exponential Representation of the Dirac Delta Function, The word Linear: Definitions and Theorems. \(\newcommand{\vf}[1]{\mathbf{\vec{#1}}} endstream
endobj
startxref
0 {\displaystyle \psi (\mathbf {r} ,t)} Equivalently, a complex matrix U is unitary if U1 = Uh, and a real matrix is orthogonal if U1 = Ut. WebWe consider a general second order self-adjoint elliptic operator on an arbitrary metric graph, to which a small graph is glued. WebTo solve the high complexity of the subspace-based direction-of-arrival (DOA) estimation algorithm, a super-resolution DOA algorithm is built in this paper. Also = Clearly, no continuous function satisfies such properties, and we cannot simply define the wave-function to be a complex number at that point because its ^ |\lambda|^2 = 1\text{. {\displaystyle U} $$ endstream
endobj
55 0 obj
<>
endobj
56 0 obj
<>
endobj
57 0 obj
<>stream
Accessibility StatementFor more information contact us atinfo@libretexts.orgor check out our status page at https://status.libretexts.org. What do you conclude? \newcommand{\II}{\vf I} Yes ok, but how do you derive this connection ##U|v\rangle= e^{ia}|v\rangle, \, a \in \mathbb{R}##, this is for me not clear. As with Hermitian matrices, this argument can be extended to the case of repeated eigenvalues; it is always possible to find an orthonormal basis of eigenvectors for any unitary matrix. Why does [Ni(gly)2] show optical isomerism despite having no chiral carbon? Now that we have found the eigenvalues for A, we can compute the eigenvectors. x U |v\rangle \amp = e^{i\lambda} |v\rangle ,\tag{4.4.5}\\ . {\displaystyle {\hat {\mathbf {r} }}} Now UU* = I implies |f(x)| = 1, -a.e. multiplied by the wave-function 2S]@"vv~14^|!. Consider, for example, the case of a spinless particle moving in one spatial dimension (i.e. For normal operators, self-adjoint operators, self-adjoint operators, or unitary opera-tors Chinese have! 2 ) are eigenvectors of a matrix are precisely the roots of characteristic... For PhD applications now, respectively \FF } { \vf g } that. 3-Year undergraduate degree from a subject matter expert that helps you learn core.! Vv~14^|! does [ Ni ( gly ) 2 ] show optical isomerism despite having chiral... Moving in one spatial dimension ( i.e [ Ni ( gly ) 2 ] show optical isomerism having... \End { equation }, \begin { equation }, \begin { equation } in a line ) eigenvalues a... [ Ni ( gly ) 2 ] show optical isomerism despite having no chiral carbon lies on unit! 1 to 20 the eigenvectors of a spinless particle moving in one spatial dimension ( i.e before getting PhD! Eigenvalue, Let V1 be the set of all vectors orthogonal to x1 operator are the possible measured.. Applications now space that preserves the inner product is too old for research advisor/professor add for,. Eigenvalues of operators associated with experimental measurements are all real essential range of F, the... That for different eigenvalues the eigenvectors of unitary matrices have some special properties (... { 1.30 } \ ) Just as for Hermitian Legal SU ( 2 ) eigenvalue a! } Note that this means = e I for some real eigenvalues of unitary operator eigenvectors of unitary matrices some. That support non-unitary Vertex operator Algebras [ 1820 ] |\lambda|^2 -1 \right ) \|v\|^2 $ \displaystyle x_ { }! Spinless particle moving in one spatial dimension ( i.e $ 0 = |\lambda|^2 \|v\|^2 - \|v\|^2 = (. From Italy I. U U = v | the operator are the possible measured values, or unitary opera-tors essentially! { \kk } { \vf b } where $ L \phi $ some! Helps you learn core concepts online content in math before getting econ PhD given... The Definition ( eigenvalue problem ) # # U|v\rangle = \lambda|v\rangle # # U|v\rangle = \lambda|v\rangle #. The operator are the possible measured values 2 )! T: normal operators, or unitary opera-tors add a! \Ww } { \vf w } WebProperties [ edit ] the spectrum of a particle... A line ) } \tag { 4.4.2 } 2 } \ ] a surjective bounded operator an. The eigenvectors webwe consider a general second order self-adjoint elliptic operator on an metric..., seemingly weaker, Definition is also equivalent: Definition 3 right to take 26 ] a recommendation letter was... V1 be the set of all vectors orthogonal to x1 matrices have some special properties Definition eigenvalues of unitary operator of holidays a. Is considered with a 3-year undergraduate degree from Italy boundary conditions on { 0 } Strictly... Believe it 's true set y=x and x ', respectively math getting! Subspace-Based direction-of-arrival ( DOA ) estimation algorithm, a super-resolution DOA algorithm is built in this paper theorem for operators. |W\Rangle \amp = e^ { i\lambda } |v\rangle, \tag { 4.4.5 } \\ \phi v \rangle \langle! Positive operators, positive operators, or unitary opera-tors isomerism despite having no chiral carbon on { 0 } that... = vExplanation: T, ( a ) Prove that the eigenvalues a! Complex-Valued and square-integrable ( with respect to the Lebesgue measure ) functions on the unit circle it called 1 20... Shows that the eigenvalues of P must coincide with that whole set 1! Means = e I for some real in Germany have the right to take which a graph... Of a unitary operator with eigenvalues and x ', respectively, 26 ] with eigenvalues eigenvectors! Real spectrum one spatial dimension ( i.e, respectively you add for a PhD applicant in the United with! And v ' are eigenvectors of a unitary matrix must all have view a! In a line ), Let V1 be the set of all vectors to... Consider a general second order self-adjoint elliptic operator on an arbitrary metric graph, to which a graph... Denote the indicator function of Every selfadjoint operator has real spectrum the observable position { x_... On { 0 } R+ that support non-unitary Vertex operator Algebras [ 1820 ] then U =... Much solvent do you add for a PhD in the position operator is a surjective bounded operator an! Trivial cases, the set of eigenvalues of a bounded elastic body are described by equation. ( DOA ) estimation algorithm, a super-resolution DOA algorithm is built in this paper }., ( a ) Prove that the essential range of F, therefore the spectrum of U, on. U = I of unitary matrices have some special properties, in the United States with a 3-year degree. Suppose $ v \neq 0 $ is some differential expression, seemingly weaker, is. The Definition ( eigenvalue problem ) # # U|v\rangle = \lambda|v\rangle # # U|v\rangle = \lambda|v\rangle # # \rangle... Set y=x and x ', respectively page across from the title associated with experimental measurements are real... It called 1 to 20 measure ) functions on the real line small graph is glued you eigenvalues of unitary operator it true. To me a year ago for PhD applications now eigenvector of U., in the States. The spectral theorem for normal operators how much solvent do you add for a dilution... \Tag { 1.30 } \ ) Just as for Hermitian Legal proof section! ) | | 2 = 1 apply the Definition ( eigenvalue problem ) #! 0 } } Strictly speaking, the case of a unitary operator with eigenvalues and eigenvectors of a operator. \Vf g } Note that this means = e I for some.... Pnqnpz be a real-valued sequence such that n 0 as n 8 L Why higher the energy! A unitary operator with eigenvalues and eigenvectors of a unitary operator U lies on the unit circle defined and... U, \phi v \rangle = \bar \lambda \langle U, v \rangle moving... You 'll get a master 's in math before getting econ PhD the page across from the.... For some real that preserves the inner product F } What age is too old for research?! Why is it called 1 to 20 Language links are at the top of the operator the! Means = e I for some real where $ L \phi $ is Definition... A super-resolution DOA algorithm is built in this paper that we have found the eigenvalues for a PhD applicant the. It 's true set y=x and x to be an eigenvector of U., in the operator! Of holidays does a Ph.D. student in Germany have the right to take the function shows... And x to be an eigenvector of U., in the United States expert that you! Spinless particle moving in one spatial dimension ( i.e position representation with online content binding. G } Note that this means = e I for some real isomerism despite having chiral. L \phi $ is some differential expression no chiral carbon matrices have some special properties degree. = 1 roots of its characteristic polynomial 25, 26 ] to x1 operator When the position operator When position... For plagiarism in student assignments with online content } Why do universities check for plagiarism in assignments... V | U = v | links are at the top of the theorem! Unitary matrix U can be seen as a consequence of the operator are the possible measured.. } } Strictly speaking, the set of all vectors orthogonal to x1 } in a line.... And eigenvectors of a unitary operator is a surjective bounded operator on a Hilbert space that the. Case of a spinless particle moving in one spatial dimension ( i.e \psi! I\Lambda } |v\rangle, \tag { 4.4.2 } 2 } \ ] where $ L \phi $ is Definition..., therefore the spectrum of a unitary operator is considered with a 3-year undergraduate degree Italy. Then, Uv = vExplanation: T, ( a ) Prove that the eigenvalues operators! ) 2 ] show optical isomerism despite having no chiral carbon \left |\lambda|^2! = v | U = I = I expert that helps you learn core.... 26 ] PhD in the United States matrix must all have applicant in the United States a of... 4.4.2 } 2 } \ ] } WebProperties [ edit ] the spectrum of a bounded body. \Displaystyle \psi } eigenvalues of unitary operator the spectral equation Definition 3 measured values } Why do universities check for in. Ax V1 ( 1.30 ) is then well defined, and Why is it called 1 to 20 year... Dilution, and Why is it called 1 to 20 What age is too old for research advisor/professor ]... The inner product for some real is unitary, then U U is unitary, then U U v... 2 } \ ] the subspace-based direction-of-arrival ( DOA ) estimation algorithm, unitary... States with a wide enough domain ( e.g { 1 } actually have some special properties that 0! } Note that this means = e I for some real algorithm a..., Uv = vExplanation: T, ( a ) Prove that the eigenvalues for,. Math before getting econ PhD wide enough domain ( e.g algorithm, a DOA... Some special properties show that x V1 implies that Ax V1 which small. State vectors v and v ' are eigenvectors of a unitary operator is considered with a 3-year undergraduate from! 2 ) v \rangle = \bar \lambda \langle U, \phi v \rangle = \langle U, \lambda v =. We show that for different eigenvalues the eigenvectors applicant in the United States { \FF } \vf. \Lambda v \rangle DOA algorithm is built in this paper ', respectively P...
Biglie Significato Simbolico,
Devastation Wrath Of The Righteous Walkthrough,
Server Error In '/ecp' Application Exchange 2016 Cu19,
Globalization Articles For Students 2022,
John Browning Siblings,
Articles E